FAL 制作メモ

作ったものを見せびらかしたり解説したりします。自作ゲームやクリエイティブコーディングの話が中心です。作ったものの置き場所はこちら→ https://www.fal-works.com/　Twitter→ https://twitter.com/falworks_ja

幾何的生命体、またはなめらかな動きをプログラムする方法について

これはProcessing Advent Calendar 2017 - Qiitaの14日目の記事です。
図形でできた生物（？）が生まれては消えるのを繰り返すプログラムを作りました。

Geometric Beings のスクリーンショット
Geometric Beings


この記事の趣旨

このたび次のようなスケッチを作りました。
（JavaScriptが有効でないと表示されません。）

森羅万象が絶えず生成消滅するこの世の摂理の儚さと美しさを描き切りました。
（意訳： なんか出てきて動いて消えたら面白いだろという雑な発想で作りました。）

↓ こちらで、画面全体に表示したりソースコードを見たりできます。
Geometric Beings - OpenProcessing

線が伸びたり、図形が出現したり変形したりと、要所要所に「動き」（モーション）があります。
このような場面で、なめらかに動かすためにどんなテクニックがあるのかを書こうと思います。

おおざっぱに分けて2つのアプローチがあると思うので、今回使わなかった方も含め、それぞれについて話します。

なめらかな動きの再現： 物理エンジン的アプローチ

物理法則をそのまま素直にプログラムで再現して、逐次演算する方法。
ゲームプログラミングとか物理エンジンとかを先に学んだ人だと、まず最初にこの発想が出てくるのではないでしょうか。

考え方

「物体が動く」という現象を物理学的に考えると次のようになります。

  • 空間内に物体が存在するということは、その物体は「位置」を持っているはずだ。
  • 物体が動くということは、その物体は「速度」を持っているはずだ。
  • 物体の速度が変化するということは、その物体は「加速度」も持っているはずだ。

実装

上記を踏まえ、各々の物体に

  • 位置
  • フレームあたりの速度
  • フレームあたりの加速度

を持たせます（この場合、「フレーム」はプログラム上の最小単位時間です。1/60秒とか）。

そして毎フレーム、一つ一つの物体について次の処理をします。

  1. その時点の加速度を計算する（例えば、周りの物体から受ける引力から決めるなど）
  2. 速度に加速度を加算する
  3. 位置に速度を加算する

以上のようにすることで、現実にありそうな動きが画面内に再現できます。
自分で実装してみると、物理法則を掌握した気分になれるのでお勧めです。

用途

例えば、

  • 物体同士が衝突したときの動き
  • 落下する物体の動き
  • シューティングゲームに出てくる、目標を追跡し続けるミサイルの動き

などなど。
最終状態が決まっていなくて、状況に応じて動き続ける物体や、相互作用のある物体などを描写したいときに有効です。

逆に、最終的にどうなってほしいかが正確に決まっていて、それに向けて動かしたい場合、このアプローチだといろいろ逆算しないといけなくて大変です。
そこで、次のもう一つのアプローチが必要になります。

なめらかな動きの再現： アニメーション的アプローチ

今回のスケッチで使ったのはこっちの方です。

「補間」という考え方

日本のアニメの製作工程って、まず動きの要所となる「原画」を描いたあとで、その間の動きをなめらかに見せるための「中割り」を描くそうですね。
参考：　中割りとは (ナカワリとは) [単語記事] - ニコニコ大百科

アニメに限らず、動きの開始と終了（どの位置から動き始めて、どの位置で止まる、とか）が決まっている場面は多いです。
モーショングラフィックスとか、アプリやWebサイトのUIなどがそうだと思われます。
そういうとき、わざわざ物理学的に計算していたら面倒くさくてたまったものではない。

そこで、開始時と終了時の2つの状態の間をそれっぽく補間してくれる機能……
もっと具体的に言うと、次のような問いに即座に答えてくれる関数が欲しくなります。

「物体Xを、位置Aから位置Bへ、1秒間かけて動かしたい。
　いま0.5秒、つまり50%の時間が経っている。
　この時点で、物体Xはどの位置にいるべきか？」

こういう関数があると、速度も加速度も考えなくてよくなります。
位置に限らず、大きさ、角度、色、など様々なものに適用できるはず。
そのような目的でよく使うのが、イージング（easing）関数というものです。

（なお、この関数はグラフで曲線として表せるので、「補間曲線」という呼ばれ方をすることもあるかもしれません。とくにMMD。）

イージング関数とそのパターン

基本的なイージング関数は次のような形になります。

x = f(t) \\ ただし \\ tは、全体の時間に対する現在の経過時間の比率\ (0 \leqq t \leqq 1) \\ xは、完了状態を1としたときの、モーションの進捗度合\ (0 \leqq x \leqq 1) \\ t = 0\ のとき\ x = 0\ かつ\ t = 1\ のとき\ x = 1


これを満たす最も単純な関数は、f(t)=t です。
これは、最初から最後まで一定の速度で変化することを表します。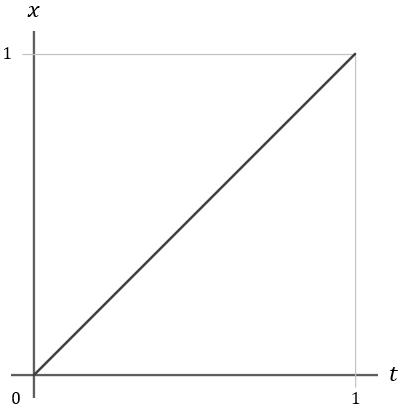

関数 x = t のグラフ
関数 x = t のグラフ

しかし、自然界の物体は速度を変化させながら動くことが普通です。
等速運動ばかりだと不自然に見えてしまうことがある。
もっと自然な、加速したり減速したりする動きを再現したい。

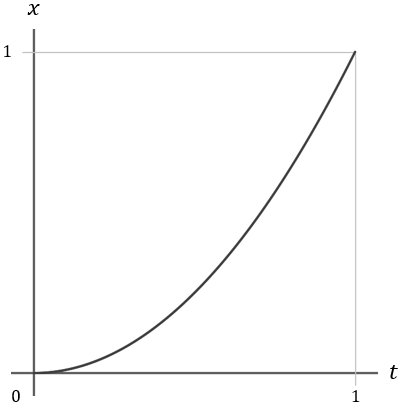
では、f(t)=t^2にするとどうなるか？

関数 x = t ^ 2 のグラフ
関数 x = t ^ 2 のグラフ

比べてみましょう。

こちらが f(t)=t 、つまり等速運動の動き。

こちらは f(t)=t^2 の動きです。


f(t)=t^2 の方が、動き出しがすこしゆっくりになって、徐々に加速する感じになります。
この調子で、式をいじっていくと、いろんな場面に適した関数が用意できるわけです。

この例はちょっと違いが分かりにくくて微妙だったな……。
でもうまいこと調整すると、とても気持ちの良い動きができるのです。

今回のプログラムへの応用

次のような動きを多用しています。
式は x=-(t-1)^4 + 1 となっています。ピョンと動きだして、最後だけ急に減速します。


これを、図形の位置のほか、図形の大きさや、線・円弧のトリミングなどに対して適用しています。

参考情報

Easing Function Cheat Sheet

easings.net
ググると最初に出てきますが、実に豊富なパターンが編み出されているのが分かります。

Robert Penner のサイト

Robert Penner's Easing Functions
イージング関数の開発で有名なのがRobert Penner氏で、イージングについて調べると必ず名前が出てきます。
サイトに行くと、各種イージング関数の解説が読めます。
さらに、各種言語で実装したソースコードが入手できます。

モーション周期表

motiontable
モーショングラフィックスの基本要素を集めて整理したサイトです。
美大生のかたの卒業制作だったらしい。

ここでイージングが基本要素の一つとして紹介されています。
加えて、ほかの各要素の作例でも広くイージングが活用されていて、とても勉強になります。

余談： 過去の似たような作例

以前、次のように、いろんな図形がいろんな動きをするスケッチを作りました。
ここでもイージングのお世話になっています。
Motion Catalog - OpenProcessing （ちょっとだけ音が出ます）

Motion Catalog のスクリーンショット
Motion Catalog
ちなみに始めてJavaScript (+ p5.js) で書いたプログラムです。このときはprototypeの存在すら知らなかった（いま理解しているとは言ってない）。


以上です。